Джироламо Саккери

Критика евклидовского обоснования геометрии, продолжалась на протяжении нескольких веков и ставшая особенно острой в 19 столетии, привела к попыткам нового дедуктивного построения геометрии, отвечающего современным требованиям науки.

Одним из ученых, предвосхитивших неевклидову геометрию, был итальянский монах Джироламо Саккери (1667 – 1733), преподававший грамматику в иезуитской коллегии в Милане. Здесь под влиянием Джованни Чевы (Джованни Чева (1648 – 1734) – итальянский инженер-гидравлик и экономист) Саккери заинтересовался математикой и стал серьезно заниматься ею. Впоследствии он преподавал математику в университете города Павши. На последнем году своей жизни Саккери опубликовал (на латинском языке) книгу под заглавием «Евклид, очищенный от всех пятен». В ней он поставил задачу исправить все недостатки («пятна») «Начал» Евклида, в первую очередь доказать V постулат. Саккери решительнее и дальше своих предшественников сделал попытку доказать этот постулат от противного.

Рассматривая четырехугольник (рис. 1), носящий его имя, Саккери стремиться доказать, что гипотезы тупого и острого углов приводит к логическим противоречиям и что остается лишь гипотеза прямого угла, из которого вытекает V постулат.

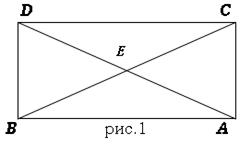
1. Он легко опровергает гипотезу тупого угла, он доказывает, что:

геометрическое место точек плоскости, равноотстоящих от данной прямой по одну сторону, не является прямой или окружностью, а другой линией (которую Лобачевский впоследствии назвал эквидистантой, то есть «равноотстоящей»);

2. две прямые, содержащиеся в одной плоскости (рис. 2), либо пересекаются в одной точке (такие прямые Лобачевский назвал «сходящимися»), либо не пересекаются, имея общий перпендикуляр, по обе стороны от которого они друг от друга удаляются («расходящиеся прямые» в терминологии Лобачевского), либо не пересекаются, удаляясь друг от друга в одном направлении и асимптотически приближаясь к другому (параллельные Лобачевского)

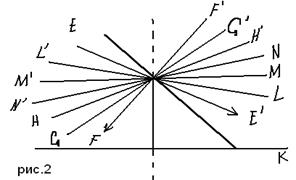
Если бы Саккери пользовался лишь логическими выводами, строгой дедукцией, то никакого противоречия он в указанных выше предложениях он не нашел бы. Однако, будучи предупрежден о невозможности того, что для евклидова постулата не имелось доказательства, Саккери для опровержения гипотезы острого угла прибег к утверждению чисто интуитивного характера: существование асимптотических прямых якобы «противоречит природе прямой линии». Заслуга Саккери состоит, разумеется, не в конечном его установлении промежуточных предложений, выведенных им на основе гипотезы острого угла, которые спустя 100 лет легли в основу новой неевклидовой геометрии Лобачевского.

Новости образования:

Графические ошибки. Технические моменты в первоначальном обучении письму
При письме имеют место следующие графические ошибки: 1. Дети при письме не соблюдают интервал между буквами в словах, неравномерно расставляют слова на строке; 2. Пишут буквы слишком размашисто или слишком узко; 3. Очень часто в работах встречается разнонаправленность наклона или чрезмерный наклон ...

Зависимость становления педагогической позиции воспитателя от уровня развития педагогических способностей
Становление педагогической позиции современного воспитателя во многом зависит от развития у него педагогических способностей. Педагог - не только профессия, суть которой транслировать знания, а высокая миссия сотворения личности, утверждения человека в человеке. В этой связи цель педагогического об ...

Детское словотворчество
Классические примеры детского словотворчества приводит К.И. Чуковский: стрекоза — «стрекозел», морщинки на лбу — «сердитки», «баюльная песня» (от слова «баюкать»), «намакаро-нился», «глазки выньми», «журчей»… Купаясь в ванне и заставляя свою куклу нырять, девочка приговаривает: «Вот притонула, а во ...