Методика проведения занятия по теме «Узлы и зацепления»

Левый и правый трилистники,- разные узлы, их нельзя продеформировать друг в друга. Под деформацией узла понимается деформация его как эластичного тела.

Вслед за трилистником по сложности идёт узел восьмёрка, своей формой напоминающей цифру 8:

Узел восьмерка

Обычно узлы рассматривают с ориентацией, т. е. считают, что задано направление обхода кривой, это направление изображается стрелкой.

Дадим математически строгое определение эквивалентности узлов. Напомним, что узел — это ломаная. С этой ломаной можно производить следующие элементарные операции

B

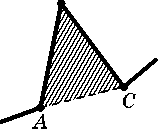
два последовательных звена AS и ВС ломаной заменить звеном АС;

звено АС заменить двузвенной ломаной АВ U ВС.

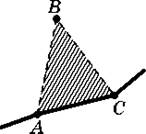
Обе операции разрешены, только если треугольник ABC не пересекается (в пространстве) ни с какими другими кусками нашего узла. Например, в ситуациях, показанных на рис. 8 (а), (б) эти операции производить можно, а в ситуации, показанной на рис. 8 (в), — нельзя.

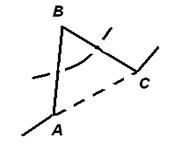
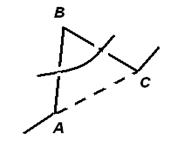
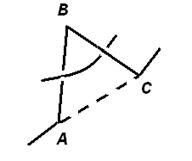
(а) (б) (в)

Рисунок 8

Определение 1. Теперь назовём два узла эквивалентными, если их можно элементарными операциями превратить в совершенно одинаковые (совмещаемые сдвигом) узлы.

Например, тривиальный узел эквивалентен плоскости окружности.

Введем еще два понятия.

Определение 2. Узлы и зацепления, которые можно продеформировать друг в друга, называют изотопными.

Определение 3. Узел называется обратимым, если он эквивалентен своему обратному, т.е. тому же узлу, проходимому в обратном направлении.

Пример. Трилистник обратим, так как направление обхода можно заменить на обратное плавным поворотом на 180° вокруг оси l.

Среди узлов, имеющих не более 8 пересечений, есть только один необратимый: это узел 817 (см. таблицу узлов в иллюстрации 3).

Распознать, обратим ли данный узел, непросто. Первое строгое доказательство необратимости было проведено только в 1962 году. Общего алгоритма для решения этой проблемы не найдено до сих пор.

Деформируя узел, его можно сильно запутать. А если даже такой простой узел как трилистник или восьмёрка, запутан не очень сильно, то распознать его бывает нелегко. Посмотрите, пожалуйста, на вторую иллюстрацию:

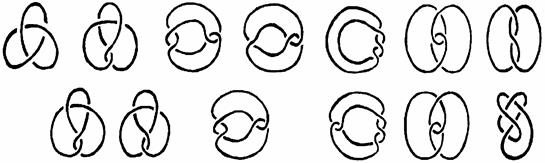
Не сразу заметно, что в верхнем углу изображён один и тот же узел (трилистник) и на нижнем ряду тоже (восьмёрка). Более того, некоторые изображения трилистника очень похожи на изображения восьмёрки.

Зацепления.

Если взять не одну нить, а несколько, и у каждой из них соединить концы, то получим зацепление.

На доске изображены три зацепления, они имеют определённые названия:

Для зацепления Хопфа существует симметрия относительно прямой, которая меняет местами нити (меняются местами компоненты зацепления). Симметрия относительно прямой в пространстве является поворотом на 180° относительно этой прямой. Поэтому существует деформация, которая меняет местами компоненты зацепления Хопфа.

Рассмотрим зацепление Уайтхеда. Перережем компоненту (нить) 1 в верхней части на нашем рисунке, затем проведём через этот разрез ту же самую нить ровно один раз и вновь соединим концы перерезанной нити. После этого, нити, из которых состоит зацепление, можно будет расцепить. Как проделать эту операцию для нити 1,- очевидно. Как сделать ту же самую операцию для нити 2 мы рассмотрим чуть позже, когда будем решать задачи.

Зацепление Борромео (такие кольца нарисованы на гербе знаменитого рода Борромео):

Зацепление Борромео имеет интересные свойства:

Эти кольца попарно не зацеплены, то есть после удаления любого кольца, остаётся пара незацеплённых колец;

Если любые два из колец Борромео зацепить простейшим образом (то есть так, чтобы они образовали зацепление Хопфа), то после этого третье кольцо можно будет снять с этого зацепления.

Существует бесконечное множество разных типов узлов и зацеплений. Типы узлов (зацеплений) принято классифицировать следующим образом. Для их классификации составляют таблицы узлов (иллюстрация 3) — перечень всех простых узлов, допускающих проекции на плоскость.

Для облегчения поиска узлы имеют стандартное обозначение: первая цифра указывает число пересечений, а вторая (расположенная в индексе) — порядковый номер узла.

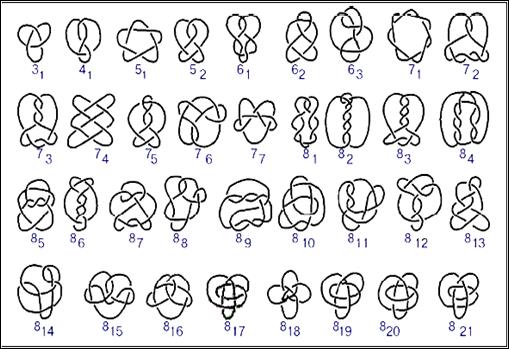
Новости образования:

Проблемное обучение как психолого-педагогический феномен
Проблемное обучение - это не абсолютно новое явление в педагогике. Элементы проблемного обучения можно увидеть в эвристических беседах Сократа, в разработках уроков для Эмиля у Жан Жака Руссо. Особенно близко подходил к этой идее К.Д.Ушинский. Он, например, писал, что лучшим способом перевода механ ...

Анализ результатов деятельности сферы образования
Отмечу следующие положительные тенденции в сфере образования: За рассматриваемый период наметился существенный рост в бюджетном финансировании сферы образования. За три года (2009,2010,2011) значительно выросли расходы на образование в Нижегородской области: В 2009 году на образование в Нижегородск ...

Роль образования в формировании толерантности
Актуализируется проблема условий, средств, механизмов формирования толерантного сознания. Одним из главных социальных институтов, способствующих формированию толерантной личности в современном обществе, является образование. Толерантность как особенность сознания или личностная черта не присуща чел ...