Методика проведения занятия по теме «Узлы и зацепления»

Решение задач.

Уровень А.

Задача 1. Доказать, что все узлы, изображённые на иллюстрации 2 (см. Приложение I) в нижнем ряду, можно продеформировать друг в друга.

Решение: Проще всего изготовить восьмёрку из верёвки или шнурка, а затем попытаться получить из этого узла все узлы, изображенные на иллюстрации в нижнем ряду. Выполнить некоторые преобразования узла восьмёрка поможет данный рисунок (на доске) [26]:

Задача 2. Доказать, что все узлы, изображённые на иллюстрации 2 в верхнем ряду, можно продеформировать друг в друга.

Решение: Можно изготовить трилистник из верёвки или нити, а затем попытаться получить из этих узлов все узлы, изображённые на данной иллюстрации.

Задача 3. Расположите зацепление Уайтхеда так, чтобы его компоненты были симметричны относительно некоторой прямой.

Решение [26]:

Задача 4. Узел называют зеркальным, если он эквивалентен своему зеркальному отражению (т.е образу при симметрии относительно плоскости). Докажите, что узел восьмерка зеркален.

Решение [27]:

Задача5. Докажите, что узел восьмерка обратим.

Решение: Узел восьмерка обратим, так как направление обхода можно заменить на обратное плавным поворотом на 180° вокруг оси.

Задача 6. Проделать для компоненты 2 зацепления Уайтхеда операцию перерезания и соединения концов перерезанной нити.

Решение: Проведём нить через разрез, как показано на рисунке 1 в иллюстрации 4. Процесс расцепления верёвок можно изобразить так, как это изображено на рисунках 2-6 в данной иллюстрации [26].

Задача 7. Докажите, что все зацепления, изображенные на рисунке, попарно изотопны (т.е. все эти диаграммы изображают зацепление Уайтхеда).

Решение: Можно сделать из одной или нескольких веревок данный узел или зацепление, расположить его на столе в виде данной диаграммы а затем попытаться получить из него другую диаграмму.

Задача 8. Доказать второе свойство зацеплений Борромео.

Решение: Кольца Борромео попарно не зацеплены, поэтому два кольца можно развести в разные стороны. Третье при этом как-то обовьётся вокруг них. Нарисуем, как именно оно будет расположено. Для этого, выясним сначала, что происходит с верёвкой, проходящей между двумя прутами, при перестановке этих прутов, в процессе которой прут 2 проходит над прутом 1:

Теперь легко понять, что происходит с третьим кольцом Борромео при разведении двух колец в разные стороны:

Будем считать, что те два кольца, которые мы раздвинули, представляют собой жёсткие обручи с какими-либо устройствами, позволяющие при желании сцеплять и расцеплять их (например, с развинчивающимися цилиндрами), а третье кольцо представляет собой верёвку. При этом верёвку снять с обручей нельзя:

Но если мы зацепим обручи, то верёвку можно будет снять:

В самом деле, на данном рисунке (на доске) изображено то же самое зацепление, что и на рисунке с зацеплением Борромео [26].

Уровень В.

Задача 9. Что получится после разрезания по средней линии ленты с тремя полуоборотами? Что получится после повторения этой процедуры?

Решение: Прежде всего, отметим, что краем скрученной ленты служит трилистник. После первого разреза получим двустороннюю поверхность, ограниченную двумя трилистниками (которые зацеплены друг с другом). После второго разреза получим две двусторонние ленты в виде трилистника, которые будут зацеплены друг с другом. Разрезав обе эти ленты, получим 4 двусторонние ленты в виде трилистника, зацепленные друг с другом. На п-м шаге получим 2n-1 зацепленных лент в виде трилистника [27].

Задача 10. Линяя А (рисунок) не разрезает тор Т на две части, а линия С разрезает. Изотопны ли А и С в фигуре Т? Изотопны ли А и С в трехмерном пространстве?

Задача 11. Докажите, что меридиан А и параллель В тора Т (см. рис. Задачи 10) изотопны в Т.

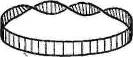
Задача 13. Докажите, что трижды перекрученная лента (рисунок) гомеоморфна ленте Мёбиуса, а ее край изотопен простому узлу.

Домашнее задание.

Задачи: 2, 5, 6, 11, 13.

Новости образования:

Результаты констатирующего эксперимента
Результаты анкетирования проведенного нами с целью выяснения отношения младших школьников к использованию дидактических игр на уроках дал следующие результаты (См. диаграмму №1-№5): Диаграмма №1 Какие уроки ты больше всего любишь? Диаграмма №2 Если бы ты был учителем, чего больше было бы у тебя на ...

Выбор технологии программирования для учебного процесса
Выбирая стратегию преподавания информатики в школе, необходимо учитывать, что задача общеобразовательного курса – это в большой степени выработка определенного стиля мышления, формирование наиболее общих навыков, умений и представлений, нежели освоение тех или иных конкретных языков и технических с ...

Выбор и обоснование методик развития мнемических способностей у учащихся
В современной психологии все отдельные опыты с памятью человека сводятся, в основном, к тому, что испытуемый тем или иным способом усваивает материал, а затем, спустя некоторое количество времени, его воспроизводит, узнаёт усвоенное. В каждом из таких опытов экспериментатор имеет дело с тремя основ ...