А.М.Лежандра

Построим на стороне BC вне треугольника ABC треугольник BCD, равный ABC, и проведем через точку D прямую, пересекающую стороны AB и AC угла BAC в точках M и N. В таком случае сумма углов треугольника BCD также равна 180°- α, а у треугольников BDM и CDN суммы углов не превосходят 180° (теорема 1).

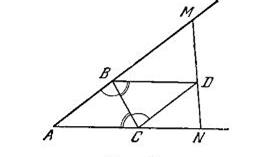
Поэтому сумма 12 углов четырех треугольников: ABC, BCD, BDM и CDN не превосходит 720°-2α. Но суммы трех углов при точках B, C и D равны 180°; поэтому сумма оставшихся трех углов при вершинах A, M и N не превосходит (720°-2α) - 540° = 180°- 2α. Таким образом, мы построили треугольник AMN, сумма угол которого не превосходит 180°-2α. Далее таким же способом строим треугольник, сумма углов которого не превосходит 180°- 4α, затем треугольник, сумма углов которого не превосходит 180°- 8α, и т. д. Но таким путем мы, в конце концов, придем к треугольнику с отрицательной суммой углов, - а такого треугольника явно не может быть! Полученное противоречие и доказывает, что сумма углов любого треугольника равна 180°, а значит (теорема 3), V постулат имеет место.

Ошибочность этого доказательства состоит в том, что Лежандр, не оговаривая этого явно, пользуется следующим утверждением: через любую точку D, взятую внутри угла CAB, можно провести прямую, пересекающую обе стороны этого угла. Но это предложение эквивалентно самому V постулату: его так же не удается доказать, исходя из остальных аксиом, как и V постулат.

Неевклидова геометрия Лобачевского и абсолютная геометрия. Многие попытки доказательства V постулата проводились по схеме "доказательства от противного", т. е. предполагалось, что V постулат не имеет места, и делался ряд выводов, имеющих место в этом случае. Если бы при этом удалось прийти к противоречию, то V постулат был бы доказан. По этому пути шли упомянутые выше Хасан ибн ал-Хайсам и Омар Хайям, а также во многом следовавшие за Хайямом азербайджанский математик XIII века Насир Ад-Дин ат-Туси, итальянский математик XVII-XVIII веков Джироламо Саккери и немецкий математик XVIII века Иоганн Генрих Ламберт.

При этом было накоплено много фактов, которые имели бы место в геометрии, в которой верны все аксиомы евклидовой геометрии, кроме аксиомы о параллельности, а последняя неверна. Особенно много удивительных теорем, которые имели бы место в такой "геометрии", если бы только последняя была возможна, получил И.Г. Ламберт. Однако никто из перечисленных выше математиков не допускал и мысли о том, что, помимо геометрии Евклида, возможна другая непротиворечивая геометрия. В большинстве случаев все их построения завершались тем, что явно или неявно применялась аксиома, содержащая утверждение, равносильное V постулату, в результате чего и обнаруживалось противоречие. Однако сегодня мы ценим упомянутые исследования как заложившие начала неевклидовой геометрии Лобачевского. Под этим названием понимается та совокупность теорем, которая может быть выведена из системы аксиом, получаемой, если заменить аксиому параллельных евклидовой геометрии противоположным утверждением: в плоскости через точку A, не принадлежащую прямой a, можно провести более одной прямой, не пересекающейся с a (см. рис.).

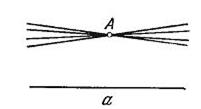
Эта геометрическая система носит имя Николая Ивановича Лобачевского, профессора и ректора Казанского университета. Независимо от него, существование новой геометрии установили великий немецкий математик Карл Фридрих Гаусс и замечательный венгерский математик Янош Бойяи, сун Фаркаша Бойяи. Названные три автора первоначально шли тем путем, который мы указали выше. Стремясь доказать V постулат от противного, они глубоко развили аксиоматическую систему, получающуюся при отрицании истинности V постулата, но не обнаружили при этом никаких противоречий. Однако, в противоположность своим предшественникам, эти три великих математика сделали из полученных ими результатов вывод о существовании геометрической системы, отличной от евклидовой.

Новости образования:

Выбор технологии программирования для учебного процесса
Выбирая стратегию преподавания информатики в школе, необходимо учитывать, что задача общеобразовательного курса – это в большой степени выработка определенного стиля мышления, формирование наиболее общих навыков, умений и представлений, нежели освоение тех или иных конкретных языков и технических с ...

Образование как общечеловеческая ценность
Признание образования в качестве общечеловеческой ценности сегодня ни у кого не вызывает сомнения. Это подтверждается конституционально закрепленным в большинстве стран правом человека на образование. Его реализация обеспечивается существующими в том или ином государстве системами образования, кото ...

Задачи и содержание работы по формированию грамматического строя речи
Термин «грамматика» употребляется в языкознании в двух значениях: он обозначает, во-первых, грамматический строй языка, во-вторых, науку, свод правил об изменении слов и их сочетании в предложении. Методика развития речи рассматривает вопросы усвоения детьми в речевой практике именно грамматическог ...