А.М.Лежандра

Французский математик и педагог А. М. Лежандр является автором замечательного школьного учебника "Начала геометрии", вышедшего в свет первым изданием в 1794 году и переиздававшегося при жизни автора 14 раз. Лежандр весьма существенно менял свою книгу от издания к изданию. При этом больше всего его заботила теория параллельных. Во всех прижизненных изданиях "Начал геометрии", кроме 9, 10 и 11-го, Лежандр доказывал V постулат, меняя, однако, доказательства от издания к изданию. Объяснялось это тем, что каждый раз после выхода очередного издания Лежандр обнаруживал ошибку в опубликованном доказательстве (точнее, не ошибку, а неявное использование утверждения, эквивалентного V постулату). Безупречного доказательства V постулата Лежандр так и не получил (и, как будет ясно из сказанного ниже, не мог получить). Однако его исследования очень поучительны и, что самое главное, вскрывают глубокие связи между V постулатом и другими предложениями. Особенно важны три замечательные теоремы Лежандра о связи V постулата с теоремами о сумме углов треугольника. Рассмотрим их подробнее. Доказательства этих теорем проводятся без использования V постулата (или аксиомы о параллельных).

Теорема 1. Во всяком треугольнике сумма внутренних углов не превосходит 180°.

Доказательство. Предположим, что наша теорема неверна, т. е. что существует треугольник ABA1, сумма углов которого больше 180°. Продолжим сторону AA1 этого треугольника и построим на прямой AA1 ряд треугольников A1B1A2, A2B2A3, ., An-1Bn-1An, AnBnAn+1, равных треугольнику ABA1; точки B и B1, B1 и B2, ., Bn-1 и Bn соединим отрезками (см. рис.); заметьте, мы не утверждаем, что отрезки BB1, B1B2, ., Bn-1Bn составляют прямую линию, - доказать это, не опираясь на V постулат, невозможно).

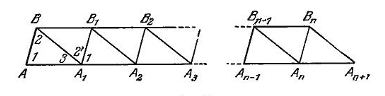
Так на рисунке ∟1+∟2+∟3>1800, а ∟1+∟2’+∟3=1800, то ∟2’<∟2; таким образом стороны А1В и А1В1 треугольника А1ВВ1 соответственно равны сторонам ВА1 и ВА треугольника АВА1, а заключенный между ними угол А1 меньше угла В. отсюда вытекает, что АА1>ВВ1 (заметим, что теорема о двух треугольниках, имеющих по две равные стороны, во всех учебниках геометрии доказывается до аксиомы параллельности, следовательно не зависит от V постулата).

Но, очевидно, не только Δ АВА1=ΔА1 А1В1А2=…=ΔАnВnАn+1, но и ΔВА1В1=ΔВ1А2В2=…= ΔВn-1AnBn. Поэтому, если положить АА1-ВВ1=а, то получим ААn –(ВВ1+В1В2+…+В n-1Bn)= na. Выбрав теперь число n настолько большим, что na>2АВ, мы найдем, что (АВ+ВВ1+В1В2+…+ В n-1Bn+BnAn)-АAn=АВ+ BnAn- na<0, т.е. что отрезок ААn больше ломаной АВВ1… BnAn, соединяющей его концы. Но последнее невозможно (причем невозможность эта устанавливается без обращения к аксиоме параллельности). Полученное противоречие и доказывает теорему.

Теорема 2. Если у какого-либо одного треугольника сумма углов равна 180°, то она равна 180° и у любого треугольника.

Доказательство. Установим прежде всего, что если сумма углов прямоугольного треугольника ABC равна 180°, то сумма углов прямоугольного треугольника ABC1, катет BC1 которого равен 2BC (см.рис.), также равна 180°.

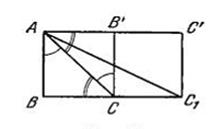
Для доказательства построим на стороне АС треугольника АСВ’, равный АСВ (причем ∟АСВ=∟В’СА, ∟ВСА=∟САВ’); в таком случае все углы четырехугольника АВСВ’ будут прямыми( так как сумма острых углов треугольника АВС по предположению равна 900). Продолжив теперь отрезок АВ’ на расстояние В’C’=АВ’ и соединив С’ с С1, получим четырехугольник В’СС1С’, равный АВС1С’ с четырьмя прямыми углами; диагональ АС1 разбивает его на два прямоугольных треугольника, сумма углов каждого из которых равна 1800.

Далее покажем, что если в одном прямоугольном треугольнике АВС сумма углов равна 1800, то сумма углов и любого другого прямоугольного треугольника А1В1С1 равна 1800. мы можем считать, что оба катета треугольника АВС больше соответствующих катетов треугольника А1В1С1; если бы это было не так, то мы добились бы нужного нам положения вещей, последовательно удвоив несколько раз катеты треугольника АВС (ведь по доказанному выше, при удвоении одного из катетов прямоугольного треугольника с сумой углов 1800 сумма его углов не меняется). Наложим теперь треугольник А1В1С1 на треугольник АВС так, чтобы у них совпали прямые углы (см. рис.), и проведем отрезок АС1.

Новости образования:

Система заданий по теме «Моделирование и формализация»
Учитывая возрастные особенности младшего школьного возраста, все выше перечисленные требования к заданиям и формы организации учебной деятельности, мы предлагаем следующую систему заданий по теме «Моделирование и формализация». Данную систему заданий целесообразно использовать для преподавания лини ...

Результаты информатизации российского образования
В целом широкому распространению современных информационных технологий в российских образовательных учреждениях мешает устаревшая и слабая материальная база информатизации образования, крайне недостаточное количество в Интернете русскоязычных образовательных ресурсов, неподготовленность педагогичес ...

Цели, задачи и содержание патриотического воспитания подростков во внеучебное время
Ильина Т.А внеклассной работой называет воспитательную работу, проводимую классными руководителями и учителями-предметниками с учащимися своей школы. [ 9 ] Советова Е.В. считает, внеурочная деятельность школьников – понятие, объединяющее все виды деятельности школьников (кроме учебной), в которых в ...