Методика проведения занятия по теме «Двумерные поверхности»

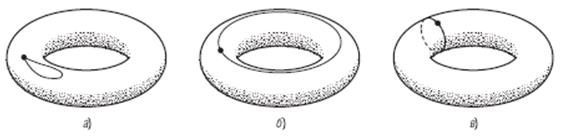
Задача 2. Докажите, что если из проективной плоскости вырезать круг, то в результате получится фигура, гомеоморфная листу Мёбиуса.

Решение: На рисунке показано, как можно представить проективную плоскость с вырезанным диском. Сделаем разрезы b и c. Затем склеим стрелки а. В результате получим лист Мёбиуса [26].

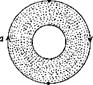
Задача 3. Докажите, что проективная плоскость гомеоморфна сфере с одним листом Мёбиуса.

Решение: Изобразим проективную плоскость, затем преобразуем её. Сначала вырежем круг, затем распрямим стрелки для получения развёртки листа Мёбиуса. В результате получим сферу с отверстием, в которое можно «поместить» лист Мёбиуса [32]:

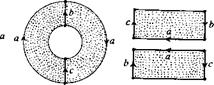
Задача 4. Докажите, что бутылку Клейна можно разрезать на 2 листа Мёбиуса.

Решение: Два способа склейки бутылки Клейна из квадрата изображены на рис.9. На рис. 10 пунктиром изображены требуемые разрезы для обоих способов склейки [25].

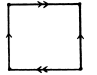
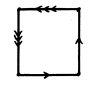
Рисунок 9

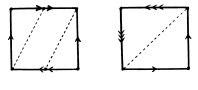
Рисунок 10

Задача 5. Докажите, что если из проективной плоскости вырезать диск, то получится лист Мёбиуса.

Задача 6. Докажите, что кольцо гомеоморфно цилиндру.

Задача 7. Проверьте, что цилиндр, тор, сфера – ориентируемые поверхности, а проективная плоскость неориентируема.

Задача 8. Докажите, что фигура, являющаяся объединением боковой поверхности цилиндра и его нижнего основания («стакан»), гомеоморфна кругу.

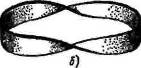
Задача 9. Докажите, что фигуры, изображенные на рисунке (лента, гомеоморфная боковой поверхности цилиндра, и дважды перекрученная лента) гомеоморфны между собой.

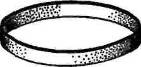
Уровень В.

Задача 10. Докажите, что сфера, к которой приклеены 3 листа Мёбиуса, гомеоморфна сфере, к которой приклеена одна ручка и один лист Мёбиуса.

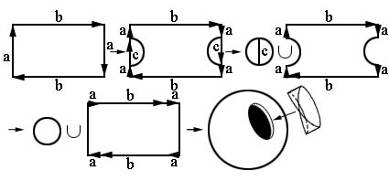
Решение: Сфера, к которой приклеены два листа Мёбиуса, гомеоморфна бутылке Клейна. Поэтому сфера, к которой приклеены три листа Мёбиуса, гомеоморфна бутылке Клейна к которой приклеен один лист Мёбиуса. Такая фигура изображена на рис.11 (а). Сделаем разрез с, а затем склеим стрелки b(рис. 11 (б)). В результате получим сферу к которой приклеены ручка а и лист Мёбиуса с [25].

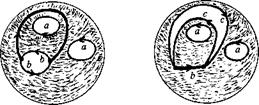
(а) (б)

Рисунок 11

Задача 11. Доказать, что сфера, к которой приклеены два листа Мёбиуса, гомеоморфна бутылке Клейна.

Решение:

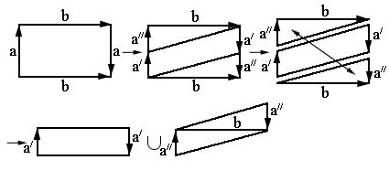
Очевидно, что склейка двух листов Мёбиуса по их общему краю эквивалентна вклеиванию этих листов в сферу с двумя дырками [32].

Задача 12. Докажите, что замкнутая ориентируемая двумерная поверхность не может быть гомеоморфна замкнутой неориентируемой двумерной поверхности.

Задача 13. К сфере с двумя дырами приклейте цилиндр по его краям. Докажите, что полученная поверхность гомеоморфна сфере с приклеенной ручкой, т.е. тору.

Задача 14. Покажите, что кольцо и лист Мёбиуса можно получить из круга приклеивание к его границе прямоугольника по двум сторонам.

Задача 15. В шаре высверлены три сквозных цилиндрических отверстия, не соединяющихся между собой. Докажите, что поверхность получившегося тела гомеоморфна сфере с тремя ручками.

Задача 16. В шаре высверлены три сквозных цилиндрических отверстия, оси которых проходят через центр шара. Докажите, что поверхность получившегося тела гомеоморфна сфере с пятью ручками.

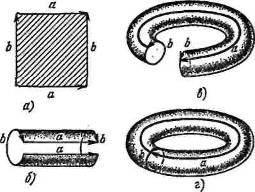
Задача 17. Если попарно склеить противоположные стороны квадрата с учетом указанных на рисунке а направлений, то получится тор (рисунок б, в, г). Какая поверхность получится, если склеивание произвести с учетом направлений на рисунке (сторона с остается не склеенной)?

Новости образования:

Анализ методик коррекции активного и пассивного словаря у дошкольников с ОНР
В современной методике словарная работа рассматривается как целенаправленная педагогическая деятельность, обеспечивающая эффективное освоение словарного состава родного языка. Развитие словаря понимается как длительный процесс количественного накопления слов, освоения их социально закрепленных знач ...

Средства и формы музейной деятельности: эффективностьвоздействия на личность
Рассмотренные в предыдущем параграфе особенности музейной коммуникации с точки зрения возможностей включения музея в педагогический процесс общества расширяют возможности воспитательной деятельности общества через использование инструментов музейной деятельности. Сегодня включение форм и средств му ...

Понятие общения в психологической и педагогической теории
Проблема слова, речи, искусства воздействия говорящего на слушателей имеет давнюю, насчитывающую более двадцати столетий историю. Многие важные вопросы этой проблемы были в самом общем виде поставлены и рассмотрены еще Цицероном. Именно ему принадлежит заслуга определения основных коммуникативных з ...