Характеристика задач на построение

В преподавании математики большое значение при­обретают вопросы, связанные с обучением учащихся геометрическим построениям (выполнение наиболее рас­пространенных геометрических построений и обучение решению задач на построение).

Решая задачи на построение, учащиеся приобретают первые теоретические и практические основы «графической грамотности», знакомятся с наиболее употребитель­ными приемами их решения, с инструментами, исполь­зуемыми в различных условиях работы (о чертежно-конструкторской практике, при разметке, при выполне­нии построений на местности). У них развиваются пространственное воображение, конструктивные способно­сти, сообразительность, изобретательность, т. е. такие качества, которые необходимы работникам многих про­фессий.

Доказательство правильности решения задачи и ее исследование способствуют лучшему усвоению учащими­ся теоретического материала, развитию их логического мышления.

Обучение геометрическим построениям в школе имело до последнего времени много недостатков. Так, уча­щиеся поздно знакомились с геометрическими построениями (в VI классе ими занимались лишь в конце учебного года). Приемы решения задач на построение часто не отвечали требованиям практики: как правило, изуча­лись построения, выполняемые только циркулем и линейкой, а другие чертежные инструменты практически не использовались; мало уделялось внимания распространенным построениям, хотя обоснование их соот­ветствовало программе по геометрии и целесообразность применения этих построений на уроках математики, чер­чения и других предметов не вызывала сомнения; при рассмотрении геометрических построений не уделялось должного внимания установлению связи между приема­ми построений (на бумаге, при разметке, на местности) и использованием соответствующих инструментов.

Задачей на построение называется предложение, ука­зывающее, по каким данным, какими средствами (инст­рументами) и какой геометрический образ (точку, пря­мую, окружность, треугольник, совокупность точек и т. д.) требуется найти (начертить, построить на плоскости, на­метить на местности и т. п.) так, чтобы этот образ удо­влетворял определенным условиям.

Будем считать средствами построения циркуль и одно­стороннюю линейку; вопрос о дополнении этих инстру­ментов чертежным прямоугольным треугольником будет рассмотрен далее.

Задача на построение может быть выражена с по­мощью чертежа-задания. Чертеж-задание включа­ет в себя данные элементы и требование задачи. Рассмот­рим примеры.

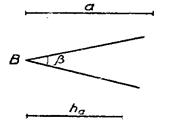
1. Построить треугольник по основанию а, углу при основании В=β и высоте на основание hа (рис.6)

2. Построить окружность данного радиуса r, проходящую через две данные точки А и В (рис.7).

Чертеж-задание выделяет из элементов плоскости данные элементы. При этом возможны два случая: 1) дан­ные элементы являются уже построенными (пример 2, точки А и В), и в этом случае перемещение их по пло­скости невозможно (данные элементы определены по по­ложению); 2) данные элементы лишь могут быть постро­ены (пример 1 – отрезки а и hа, угол В, пример 2 – от­резок r); в этом случае подразумевается, что элементы могут быть построены в «любом месте» плоскости (дан­ные элементы не определены по положению).

Решить задачу на построение при помощи циркуля и линейки – значит свести ее к конечной сово­купности пяти элементарных построений, которые заранее считаются выполнимыми:

1) построение прямой линии через две известные точки:

Дано: Дано:

Построить треугольник Построить окружность

АВС радиуса r, проходящую

через точки А и В

Рис. 6 Рис. 7

2) построение точки пересечения двух известных пря­мых (если эта точка существует);

3) построение окружности известного радиуса с цент­ром в известной точке;

4) построение точек пересечения известной прямой и известной окружности (если эти точки существуют);

5) построение точек пересечения двух известных окружностей (если такие точки существуют).

Термин «известный элемент» означает, что этот элемент либо дан, либо получен в предыдущих построениях, либо выбран произвольно.

Сведения к каждой задаче к элементарным построениям практически неудобно, так как делает решение громоздким. Иногда удобнее сводить задачи к так называемым основным построениям. Выбор некоторых построений в качестве основных в известной мере произволен.

Новости образования:

Игра- как средство формирования личности дошкольника
Основной вид деятельности детей дошкольного возраста - игра, в процессе которой развиваются духовные и физические силы ребенка: его внимание, память, воображение, дисциплинированность, ловкость. Кроме того, игра – это своеобразный, свойственный дошкольному возрасту способ усвоения общественного опы ...

Принципы организации внеурочной работы по учебным предметам
В.И. Казаренков выделил следующие принципы организации внеурочных занятий подростков и старшеклассников по учебным предметам: ¾ взаимосвязь внеурочных и урочных занятий; ¾ демократизация жизнедеятельности учащихся; ¾ гуманизация отношений между участниками педагогического проце ...

Источники формирования самооценки в младшем школьном возрасте
самооценка младший школьный ценностный Самооценка является важным компонентом развития самосознания личности, то есть осознания человеком собственных умственных способностей, физических сил, поведения и мотивов, своего отношения к окружающим и к самому себе. Проблема развития самооценки у школьнико ...