Характеристика задач на построение

Характеристика чертежа-задания показывает, что за­дачи на построение делятся на два существенно различ­ных вида:

Задачи «метрические», в которых требуется построить геометрический образ по данным элементам, имеющим определенные размеры, но не определенными по положению на плоскости. Следовательно, и требуемый в задаче геометрический образ может занимать произволь­ное положение на плоскости (пример 1).

Задачи «положения», в которых построение требуемого геометрического образа выполняется на осно­ве данных элементов, из которых хотя бы один определен по положению на плоскости. Следовательно, и требуемый геометрический образ должен занимать определенное по­ложение на плоскости (относительно данных элементов, пример 2).

В теории геометрических построений каждый инстру­мент выполняет свойственную только ему операцию. Описание этой операции является его абстрактной характеристикой и дает возможность указать на те эле­менты чертежа, которые могут быть построены при од­нократном использовании того или иного инструмента.

Обычно на практике несколько «абстрактных» инст­рументов объединяются в один (например, чертежный треугольник является комбинацией односторонней ли­нейки, прямого и двух острых углов). Часто также один инструмент используется для выполнения двух (или не­скольких) совершенно различных операций (например, линейка используется для построения прямой, проходя­щей через две заданные точки, и общих касательных к двум данным окружностям). Это дает возможность зна­чительно сократить число используемых инструментов.

Укажем характерные операции для наиболее распро­страненных в школьной практике чертежных приборов и на те элементы чертежа, которые могут быть получены при однократном их использовании.

Циркуль. Характерная для циркуля операция – проведение окружности данным (или произвольным) ра­диусом с центром в данной (или произвольной) точке.

Таким образом, циркулем могут быть построены:

а) окружность данного радиуса с центром в данной точке (радиус может быть задан двумя точками);

б) дуга окружности данного радиуса с центром в данной точке.

Линейка. Характерная операция для чертежной линейки – проведение прямой через две дан­ные точки.

На практике линей­кой пользуются также для построения к дан­ной окружности каса­тельной (рис. 8), проходящей через за­данную вне ее точку, и для построения общих внешних и внутренних касательных к двум окружностям.

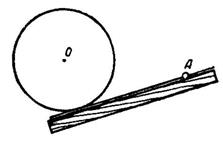
Рис. 8

Теоретически эти опе­рации так же строги, как и проведение прямой через две данные точки. Практическая точность в большинстве случаев вполне удовлетворительна. Этот прием часто используется в чертежных работах и при разметке. Итак, при помощи линейки могут быть построены:

а) прямая, проходящая через две данные точки;

б) отрезок прямой, ограниченный двумя данными точками;

в) луч, проходящий через данную точку и имеющий начало в другой данной точке;

г) касательная к данной окружности, проходящая через данную вне окружности точку;

д) внешние и внутренние касательные к двум данным окружностям.

Чертежный треугольник обладает всеми свойствами односторонней линейки. Следовательно, с помощью чертежного треугольника могут быть получены те же элементы, что и с помощью линейки, а также прямая, проходящая через данную точку и образующая с данной прямой угол, равный одному из углов чертежного треугольника.

Транспортир. Характерной операцией для тран­спортира является построение точки, лежащей на луче, проходящем через данную на прямой точку и образующем заданный угол с этой прямой (рис. 9).

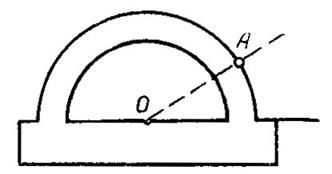
Рис. 9

Абстрактная характеристика каждого инструмента может быть использованы для выяснения вопроса о разрешимости задач на построение теми или ины­ми инструментами.

С этой целью в теорию геометрических построе­ний вводится понятие класса конструктивных элементов. К этому клас­су относятся все заданные элементы, а также: прямая, если она определяется двумя конструктивными точками; окружность, если она определяется конструктивным цен­тром и конструктивным радиусом (пара конструктивных точек); точка, лежащая на луче, проходящем через за­данную на конструктивной прямой точку и образующем с этой прямой заданный угол, и, наконец, точки, являю­щиеся пересечением конструктивных линий (прямых и окружностей).

Новости образования:

Творческие работы нетрадиционных жанров
К традиционным школьным занятиям принадлежат, как известно, уроки изучения нового материала, закрепления знаний, умений и навыков, проверки и учета приобретенных знаний, умений и навыков, анализа контрольных работ, обобщения и систематизации выученного, повторение темы или раздела. Наряду с этими ф ...

Математическое мышление
Эффективность и качество обучения математике определяются не только глубиной и прочностью овладения школьниками системой математических знаний, умений и навыков, предусмотренных программой, но и уровнем их математического развития, степенью подготовки к самостоятельному овладению знаниями, сформиро ...

Общение на основе увлеченности совместной творческой деятельностью
В основе этого стиля – единство высокого профессионализма педагога и его этических установок. Ведь увлеченность совместным с учащимися творческим поиском – результат не только коммуникативной деятельности учителя, но в большей степени его отношения к педагогической деятельности в целом. Такой стиль ...