Характеристика задач на построение
Алгебраический метод.
1. Одним из важных методов, применяемых в школьном курсе геометрии, является алгебраический метод решения задач на построение. Уже в VI-VII классах учащиеся неоднократно применяли алгебру при решении задач вычислительного характера и задач на доказательство с целью упрощения решения. Алгебра дает очень удобный и хороший способ решения геометрических вопросов аналитическим путем.
 В VI классе целесообразно рассказать, что некоторые сведения по алгебре были известны еще в глубокой древности, но вопросы алгебры не отделялись от вопросов арифметики и геометрии. Позже греческие ученые, такие, как Пифагор, Евклид, которые занимались преимущественно геометрией, получили значительные результаты и в алгебре. Но многие алгебраические тождества доказывались ими геометрически. На доске в качестве примера иллюстрируем доказательство тождества: (a + b)2 = a2 + 2ab + b2 (рис. 56).
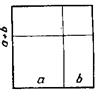
В VI классе целесообразно рассказать, что некоторые сведения по алгебре были известны еще в глубокой древности, но вопросы алгебры не отделялись от вопросов арифметики и геометрии. Позже греческие ученые, такие, как Пифагор, Евклид, которые занимались преимущественно геометрией, получили значительные результаты и в алгебре. Но многие алгебраические тождества доказывались ими геометрически. На доске в качестве примера иллюстрируем доказательство тождества: (a + b)2 = a2 + 2ab + b2 (рис. 56).
Рис. 56
Площадь квадрата, построенного на сумме отрезков а и b, равна сумме площадей двух квадратов со сторонами а и b и площадей двух прямоугольников со сторонами а и b. В IX в. н. э. узбекский
ученый Мухаммед-бен-Муса ал-Хорезми написал книгу «Хисаб ал-джебр вал-мукабала», появление которой явилось как бы моментом оформления науки алгебры. В дальнейшем алгебра получила свое самостоятельное развитие и начала оказывать большую помощь при решении различных задач других математических дисциплин, в том числе и геометрии.
2. Алгебраический метод решения задач на построение рассматривается как дальнейшее расширение применения алгебры к геометрии. Как известно, он состоит в следующем. Предположив задачу решенной: 1) Устанавливаем, какой или какие отрезки (в редких случаях углы или дуги) нужно определить, чтобы решить задачу, и обозначаем длины этих отрезков через х, y, z, ., а длины данных отрезков – через а, b, с, …, то есть вводим обозначения. 2) Из условия задачи, пользуясь известными геометрическими соотношениями между искомыми и данными отрезками, составляем уравнение или систему уравнений. 3) Решаем это уравнение или систему уравнений. 4) Исследуем полученные формулы для неизвестных отрезков по условию задачи. 5) Строим с помощью инструментов искомые отрезки, выраженные полученными формулами через данные отрезки. После того как неизвестные построены, выполняем построения, которые окончили бы решение, проводим доказательство и исследование.
Первые четыре этапа известны учащимся, так как при решении геометрических задач на вычисление и алгебраических на составление уравнений всегда выделялись такие же этапы. Это говорит о том, что задачи на построение, решаемые таким методом, можно рассматривать как обобщение задач вычислительного характера, а с другой стороны, при применении алгебраического метода всякая задача на построение заменяется вначале задачей на вычисление, так что каждая задача на построение, решаемая этим методом, является, по существу, и задачей на вычисление.
4. Целесообразность рассмотрения этого метода в средней школе не определяется только тем, что учащиеся ознакомятся с еще одним видом задач, для решения которых применяется алгебра. Алгебраический метод решения отдельных, даже сложных задач на построение более доступен учащимся, ибо достаточно получить соответствующую формулу для определения искомой величины, чтобы стало ясным все решение задачи.
Алгебраический метод позволяет легко установить условия возможности решения задачи, а также наличие определенного числа решений при тех или иных значениях и положениях данных.
5. Однако в средней школе не следует чрезмерно увлекаться этим методом за счет других важных разделов. Нужно решать доступные и интересные для учащихся задачи.
Новости образования:
Характеристика типичных ролевых позиций педагога-воспитателя
Л.Б. Ительсон дал характеристику типичных ролевых позиций педагога. Педагог может выступать в качестве: · информатора, если он ограничивается сообщением требований, норм, воззрений; · друга, если он стремится проникнуть в душу ребёнка; · диктатора, если он насильственно внедряет нормы и ценностные ...
Выбор подхода к преподаванию структурного программирования
При решении задач с использованием структурного программирования можно выделить два основных направления [7, c. 78]:1) "алгоритмический" подход заключается в следующем: схема решения задачи описывается на алгоритмическом языке (языке блок-схем алгоритмов) и затем переводится в программную ...
Сущность понятий
«здоровье», «здоровый образ жизни»
Улучшение состояния здоровья нового поколения – важнейшая задача современности, в комплексном решении которой невозможно обойтись без общеобразовательной школы. Учителям совместно с родителями, медицинскими работниками, психологами и общественностью необходимо так организовать школьную деятельность ...
Главное на сайте
- Главная
- Культура педагогического труда
- Образование и личность
- Усвоение знаний в школе
- Педагогические ценности
- Инновационные технологии в обучении
- Методика работы с текстовой информацией
- Педагогические практики

