Математическое мышление

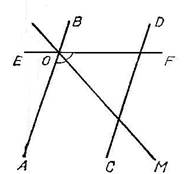
рис. 1

Параллельные прямые АВ и CD пересечены прямой EF, величина одного из внутренних углов при точке О (рис. 1 ) равна 130°. ОМ – биссектриса этого угла. Определить величину угла, обра­зованного ею с прямой CD.

Здесь прямая ОМ выступает одновременно и как биссектриса, и как секущая. Ее роль как биссектрисы угла создает функциональ­ного устойчивость, в силу которой учащиеся часто затрудняются в: использовании этой прямой в качестве секущей.

Следует отметить, что шаблонность мышления, присущая многим школьникам, имеет как негативный, так и позитивный харак­тер. Она избавляет школьника от необходимости заново усваивать те или иные операции, решать задачи тех типов, которые неодно­кратно им встречаются, безусловно, положительно сказывается на результатах обучения.

Однако шаблонность мышления мешает школьникам мыслить оригинально, отделять главное от второстепенного, отыскивать новые пути решения задач, применять известные им знания в но­вой ситуации. Понятно, что все это не способствует развитию твор­ческих потенций школьника.

Поэтому в обучении математике весьма важно помогать школьникам преодолевать этот «психологический барьер», развивать у них гибкость мышления.

Высший уровень развития нешаблонного мышления проявляет­ся в оригинальности мышления, которая в школьном обучении математике, как правило, выступает в необычности спо­собов решения известных учащимся задач. Оригинальность мышле­ния, чаще всего, проявляется как следствие глубины мышления. Глубина мышления характеризуется умением про­никать в сущность каждого из изучаемых фактов, в их взаимосвязи с другими фактами; выявлять специфические, скрытые особенности в изучаемом материале (в условии задачи, способе ее решения, ре­зультате); умением конструировать модели конкретных ситуаций. Глубину мышления нередко называют умением выделять существенное.

Известно, что познание регулируется по двум каналам отраже­ния реальной действительности (объекта познания): по весьма узкому каналу отражения самого объекта и весьма широкому ка­налу отражения его фона (совокупности связанных с этим объек­том различных свойств его самого и других, связанных с ним объ­ектов); при этом второй канал часто функционирует бессознатель­но. Это вызвано тем, что знания и опыт откладываются в памяти (и воспроизводятся в ней) своеобразными комплексами понятий и представлений – «готовыми фрагментами ответов» на соответствую­щие вопросы. В процессе воспроизведения вспоминается не только то, что требуется вспомнить, но и многие бесполезные в данной си­туации положения, так или иначе связанные в сознании с основным объектом.

Процесс отделения фона от самого объекта – сложный процесс. Величина фона в значительной степени зависит от тех условий, в которых происходит изучение объекта, равно как и от умений изу­чить этот объект в его существенных свойствах достаточно глубоко. Поэтому глубину мышления (умение выделять существенное) пра­вомерно считают качеством, формирование которого у школьников является важнейшим условием успешности обучения математике.

Таким образом, глубина мышления проявляется прежде всего в умении отделить главное от второстепенного, обнаружить логическую структуру рассуждения, отделить то, что строго доказано, от того, что принято «на веру», извлекать из математического текста главное из того, что в нем сказано (и не более того), и т.д.

Новости образования:

Примерные вопросы для проверки назначения приборов
Рассказать по рисунку действие прибора для получения водорода. Как проверить водород на чистоту? Нарисовать аппарат Киппа и рассказать, как он работает. Найти на демонстрационном столе прибор для разложения воды электрическим током и объяснить устройство и принцип его действия. Собрать из имеющихся ...

Постановка задачи исследования
Целью дипломной работы является создание современной модели web-сервиса для тестирования уровня знаний учеников по предмету математика с помощью средств web-разработки и программная реализация для эффективной работы тестовой системы. Перед формированием модели WEB-сервиса тестирования нужно четко о ...

Формы, методы и приемы работы по формированию «дизайнерского мышления» и изобразительных способностей
С целью коррекционной работы мы можем провести дидактические игры, которые помогают создать особую эмоциональную атмосферу, вызвать интерес детей к дизайнерской деятельности. Дидактические игры творческой направленности могут быть включены во все виды занятий, а могут проводиться и вне занятия во в ...