Математическое мышление

Организованность памяти дает возможность соблюдать принцип экономии в мышлении. Поэтому нецелесообразно загружать память учащихся ненужной или незначительной информацией, не накап­ливать у них опыт учебной деятельности, бесполезной для дальней­шего. Так, например, до недавнего времени школьники «разучива­ли» решения типовых текстовых задач, не имеющих большого по­знавательного значения; это весьма отрицательно сказывалось и на развитии их памяти.

Опыт показывает, что организованность памяти формируется у школьников особенно эффективно, если запоминание каких-либо фактов основано на понимании этих фактов. Поэтому зубрежка школьниками многочисленных правил является не только непро­дуктивной деятельностью, но и попросту вредной.

В процессе обучения математике развитию и укреплению памяти школьников способствуют: а) мотивация изучения; б) составление плана учебного материала, подлежащего запоминанию; в) широкое использование в процессе запоминания сравнения, аналогии, классификации и т. п.

Такие качества научного мышления, как ясность, точность, лаконичность речи и записи, не нуждаются в особых комментариях.

Специфика математического мышления проявляется не только в том, что ему присущи все качества научного мышления, но и в том, что для него характерны особые формы (разновидности проявления мышления), которые в ходе их описания обычно выделяются специальными терминами: конкретное и абстрактное мышление, функциональное мышление, интуитивное мышление и т.п.

Так как в процессе обучения математике обычно используют­ся так называемые конкретно – индуктивные или абстрактно-дедук­тивные методы обуче­ния, то, естественно, возника­ет необходимость (из дидакти­ческих соображений) говорить о конкретном (предметном) или абстрактном мышлении школьников.

Конкретное (предметное) мышление – это мышление в тесном взаимодействии с конкретной моделью объекта.

Различаются две формы конкретного мышле­ния:

1) неоперативное (наблюдение, чувственное восприя­тие);

2) оперативное (непосредственные действия с конкрет­ной моделью объекта).

Неоперативное конкретное мышление чаще всего проявляется у дошкольников и младших школьников, которые мыслят лишь наглядными образами, воспринимая мир лишь на уровне пред­ставлений. То, что школьники на этом уровне развития не владе­ют понятиями, ярко иллюстрируется опытами психологов школы Ж. Пиаже. Рассмотрим некоторые из них:

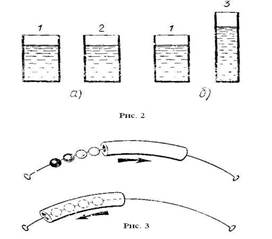
1. Детям демонстрируются два сосуда (рис. 2 , а) одинаковой формы и размеров, содержащие поровну темную жидкость. Дети легко устанавливают равенство жидкостей в первом и втором сосуде. Далее, на виду у детей жидкость из одного сосуда перели­вают в другой более высокий и узкий (рис. 2 , б) и предлагают срав­нить количество жидкости в этом сосуде и оставшемся нетронутым. Дети утверждают, что в новом сосуде жидкости стало больше.

2. Детям демонстрируют цветы: васильки и маки (например, 20 маков и 3 василька) и спрашивают, чего больше: цветов или ма­ков? И хотя дети как будто бы знают, что и васильки и маки суть цветы, они отвечают, что маков больше.

3. Через полую непрозрачную трубку (рис.3) на виду у детей пропускают проволоку с фиксированными на ней шариками (красным, белым, синим, зеленым), пока все шарики не скроются в трубке.

Дети наблюдают порядок «вхождения» шариков в трубку. Затем начинают обратное движение проволоки, предлагая детям назвать цвет шарика, который теперь выйдет первым, вторым и т. д. Дети обычно называют шарики в том порядке, в каком они «вхо­дили» в трубку.

Новости образования:

Особенности культуры педагогической деятельности
Культура человека, особенно взрослого, многоаспектна, и единое, общепризнанное понятие "культура" ¹ отсутствует. Мы под культурой понимаем "определенный уровень развития общества и человека, выраженный в типах и формах организации жизни и деятельности людей, а также в создаваемы ...

Характеристика МОУ «Большеутинская средняя общеобразовательная школа»
Муниципальное общеобразовательное учреждение «Большеутинская средняя общеобразовательная школа» расположена по адресу: 623346, Свердловская область, Ачитский район, с. Большой Ут, улица Нагорная, 1. Образовательное учреждение строит свою деятельность в соответствии с образовательной программой (70, ...

Развитие вокально-хоровых навыков у учащихся на современном этапе
Вокальное воспитание в школе – важнейшая часть всей хоровой работы в коллективе. Голос ребенка - естественный инструмент, которым он обладает с ранних лет. Вот почему пение все время присутствует в жизни ребенка, заполняет его досуг. Пение – яркая образная форма углубленного представления об окружа ...