Характеристика задач на построение

Доказательство.

1. После того как фигура построена, необходимо установить, удовлетворяет ли она условиям задачи, то есть показать, что фигура, полученная из данных элемен­тов определенным построением, удовлетворяет всем усло­виям задачи. Значит, доказательство существенно за­висит от способа построения. Одну и ту же задачу можно решать различными способами, в зависимости от наме­ченного при анализе пла­на построения, а поэтому, и доказательство в каж­дом случае будет свое, Рассмотрим задачу: «По­строить трапецию по четы­рем сторонам» (рис. 26).

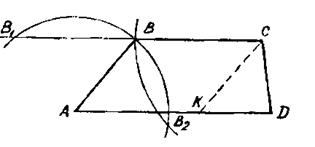Рис. 26

Проведя СК||ВА, решение задачи сводим к построению треугольника КСD по трем сторонам: две равны боковым сторонам трапеции (АК = КС), а КD = АD – ВС. Построим треугольник КСD, и, считая сторону АD построенной, допол­ним его до трапеции различными способами:

1) Проведем ВС||АD и, отложив меньшее основание, соединим полученную точку В с А Доказательство све­дется к установлению равенства: АВ = КС.

2) Если провести АВ||КС и ВС||АD, то тогда уже надо доказать, что АВ = КС и ВС = АК.

3) Если провести прямую СВ||DА и на ней найти точки В и В1, отстоящие от А на расстоянии, равном бо­ковой стороне, то в этом случае точка В1 будет посторон­ней и лишь точка В будет искомой, причем доказатель­ство (ВС = АК) уже усложняется.

4) Если отыскивать точку В, как точку пересечения окружностей (А; АВ) и (С; СВ), то из двух точек В и В2 только точка В будет искомой.

Третий и четвертый случаи подчеркивают необходи­мость доказательства. В анализе мы находим необходи­мые условия, которым должно подчиняться построение, чтобы получить искомую фигуру. Надо еще установить, что найденные необходимые условия являются и доста­точными, то есть, что построенная фигура удовлетворяет всем требованиям задачи.

2. При решении простейших задач, когда все условия задачи находят непосредственное отражение в плане по­строения, нет необходимости доказывать, что фигура, полученная из данных элементов таким построением, является искомой. Например: «Построить треугольник по двум сторонам и углу между ними». Здесь доказатель­ство сводится к простой проверке, такие ли взяли сторо­ны, как данные, и будет ли построенный угол равен дан­ному. В подобных задачах доказательство является излишним, ибо правильность решения обеспечивается соответствием построения анализу и данным условия задачи.

Но иногда не все условия отражаются в плане анали­за и при построении. Например, в случае (3) точка В действительно должна лежать на ВС и отстоять от точки А на данном расстоянии. Но этого недостаточно, так как отрезок АВ должен быть параллельным СК.

Так как доказательство зависит от избранного реше­ния, то, не ознакомившись с анализом и построением, нельзя сказать, правильно пли неправильно проведено доказательство.

3. Доказательство не просто зависит от анализа и по­строения, между ними существует взаимосвязь и взаимообусловленность. Построение проводится по пла­ну, составленному при анализе. Таких планов можно указать несколько. Построение и доказательство являют­ся своеобразным критерием правильности и рациональности составленного плана. Если план не осуществим имеющимися инструментами или же построение оказыва­ется нерациональным, мы вынуждены искать новый план решения. Аналогичным образом и доказательство, и исследование влияют на анализ, предопределяя нередко выбор плана решения.

4. Для упрощения доказательства целесообразно предлагать учащимся и такие задачи на доказательство, которые не только служат для развития математического мышления или для пополнения объема знаний, но и могут быть использованы при решении задач на построение. Например, при изучении частных видов параллелограм­ма решаем задачи:

1) Если у параллелограмма диагонали взаимно пер­пендикулярны, то такой параллелограмм есть ромб.

2) Если у параллелограмма диагональ делит один из углов пополам, то такой параллелограмм есть ромб.

3) Если у параллелограмма диагонали равны, то та­кой параллелограмм есть прямоугольник и т. п.

При решении задач на построение методом подобия, выбрав центр подобия и найдя коэффициент подобия, выполняем подобное преобразование многоугольника, подобного искомому, почти всегда не тем способом, который изложен в учебнике А. П. Киселева, и всякий раз вынуждены проводить отдельное доказательство, что по­лученный многоугольник – искомый. Целесообразно ознакомить учащихся с общепринятым способом по­строении, основанным на том, что у гомотетичных многоугольников сходственные стороны попарно параллельны. Благодаря этому при решении почти всех задач на по­строение многоугольников методом подобия доказательство, что полученный многоугольник искомый, значи­тельно упрощается.

Новости образования:

Анализ эффективности предложенной системы занятий по развитию произвольной памяти младших школьников с интеллектуальными нарушениями
Целью данного этапа эксперимента являлось: Выявление эффективности использования дидактической игры в процессе развития произвольной памяти младших школьников с интеллектуальными нарушениями. Формирование на основе полученных данных системы дидактических игр по математике, направленных на развитие ...

Организация экспериментальной работы
Согласно цели нашего исследования и поставленным задачам в настоящей главе необходимо экспериментально проверить педагогические условия моделирования духовно-творческой среды воспитания личности дошкольников. Чтобы исследовать, насколько у детей-дошкольников сформирована готовность к формированию д ...

Проблемы в сфере образования
Я выделила следующие наиболее важные проблемы, существующие в системе образования г.Н.Новгорода: 1.Высокая стоимость образовательных услуг. Услуги образования в Н.Новгороде (в 2010 году по сравнению с 2009) возросли на 7,6 проц., в том числе: дошкольного воспитания — на 25,8 %, среднего образования ...